二次域
在代数数论中,二次域是在有理数域 上次数为二的数域。二次域可以唯一地表成
上次数为二的数域。二次域可以唯一地表成 ,其中
,其中 无平方数因数。若
无平方数因数。若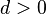 ,称之为实二次域;否则称为虚二次域或复二次域。虚实之分在于
,称之为实二次域;否则称为虚二次域或复二次域。虚实之分在于 是否为全实域
是否为全实域
二次域的 研究肇源甚早,起初是作为二次型理论的一支。二次域是代数数论的基本对象之一,虽然如此,至今仍有一些未解猜想,如类数问题。
| 单词 | Quadratic field |
| 释义 |
Quadratic field
中文百科
二次域在代数数论中,二次域是在有理数域 二次域的 研究肇源甚早,起初是作为二次型理论的一支。二次域是代数数论的基本对象之一,虽然如此,至今仍有一些未解猜想,如类数问题。
英语百科
Quadratic field 二次域In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q, the rational numbers. The map d ↦ Q(√d) is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields. If d > 0 the corresponding quadratic field is called a real quadratic field, and for d < 0 an imaginary quadratic field or complex quadratic field, corresponding to whether it is or not a subfield of the field of the real numbers. |
| 随便看 |
|
英汉网英语在线翻译词典收录了3779314条英语词汇在线翻译词条,基本涵盖了全部常用英语词汇的中英文双语翻译及用法,是英语学习的有利工具。